A Computer Scientist's Guide to Riemannian Manifold
This blog post is still under construction. I will finish the spherical manifold and 3D rotation group sections soon.
Preface
A lot of my CS friends have asked me about various Riemannian manifolds in generative modeling, especially their geometric properties that induce important concepts like exponential map and logarithm map utilized in Riemannian flow matching
Generally, I will try to avoid using too much mathematical jargon and focus on the intuition behind the concept. Nonetheless, for those who are interested in the mathematical details (like me!), I include them in the collapsible. Feel free to skip them as the main text is designed to be self-contained. As a self-taught non-mathematician in Riemannian geometry, it will be inevitable that I might make some mistake. Please email me if you find any errors or have any suggestions.
Riemannian Manifold
A manifold $\mathcal{M}$ is a space that locally looks like a flat Euclidean space everywhere. Imagine you are a tiny ant on the manifold, you will feel like you are living in a flat world, like our human being on the spherical Earth. For a smooth manifold, the tangent space $T_x\mathcal{M}$ at a specific point $x\in\mathcal{M}$ can be understood as the vector space of all possible directions (i.e., tangent vectors) one can move from $x$. The tangent bundle $T\mathcal{M}:=\bigcup_{x\in \mathcal{M}}T_x\mathcal{M}$ is defined as the union of all tangent spaces at each point. See for an illustration of the tangent space.
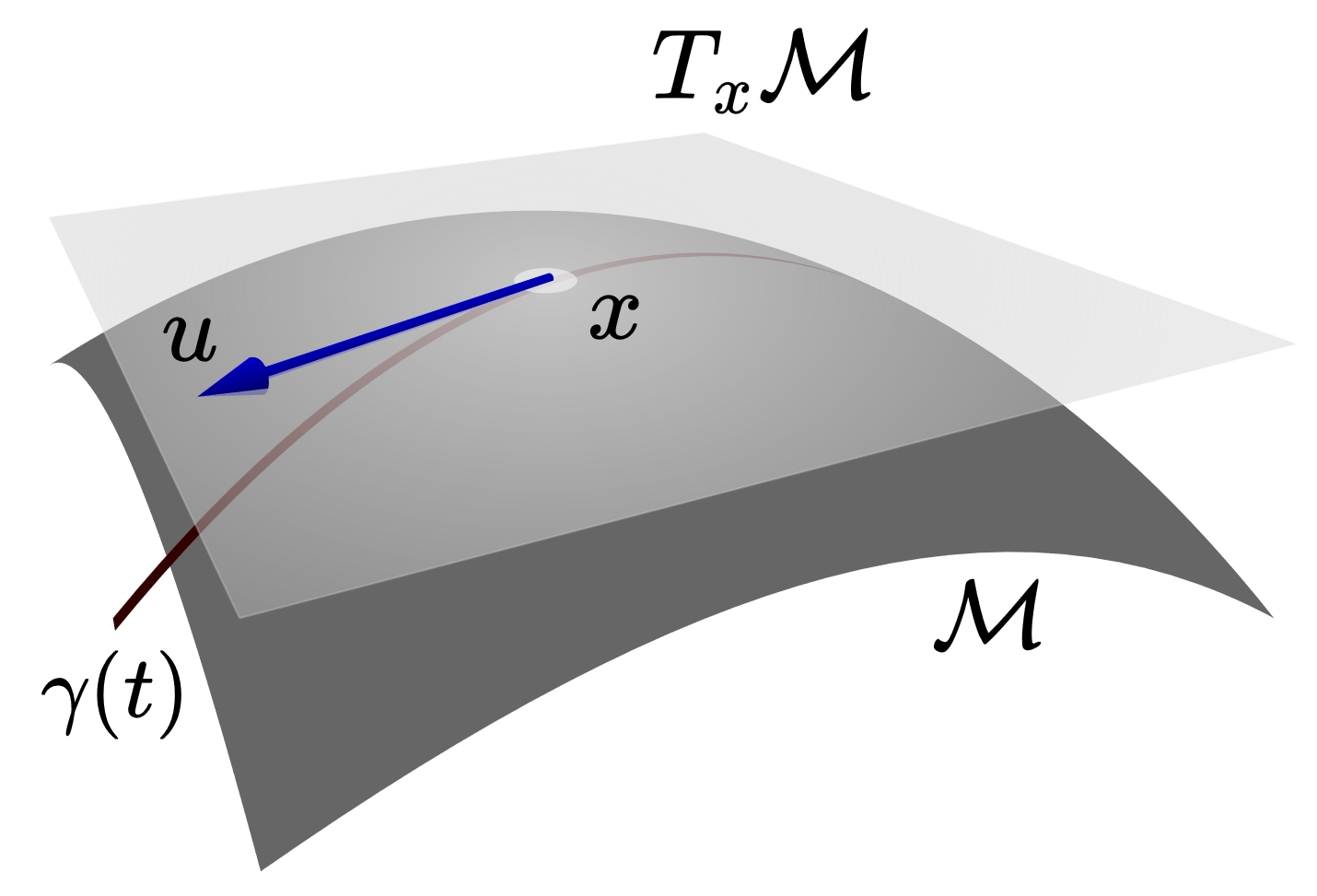
A Riemannian manifold $\mathcal{M}$ is a smooth manifold equipped with a Riemannian metric $g$, which is a smooth positive-definite inner product on the tangent space of each point: \(\begin{equation} g_x: T_x\mathcal{M}\times T_x\mathcal{M}\to \mathbb{R}. \end{equation}\) As $g$ is an inner product, we also write $\langle u,v\rangle_g:=g(u,v)$ and sometimes omit the subscript $x$ if it can be inferred from the context. However, it is important to keep in mind that the Riemannian metric depends on the point. The Riemannian norm of a tangent vector $u\in T_x\mathcal{M}$ is defined as $\|u\|_g:=\sqrt{\langle u,u\rangle_g}$. In this way, the Riemannian metric allows us to define the length of tangent vectors, which is essential for defining the distance between two points on the manifold. Recall from your calculus class for defining the infinitesimal arc length of a smooth curve as $\mathrm{d}s=\|f^\prime(t)\|_2\,\mathrm{d}t$ for a smooth curve $f:[0,T]\to\mathbb{R}^n$, the arc length of a smooth curve $\gamma(t):[0,T]\to\mathcal{M}$ on the Riemannian manifold can be calculated as: \(\begin{equation} \mathrm{d}s=\|\dot\gamma(t)\|_g\,\mathrm{d}t=\sqrt{\langle\dot\gamma(t),\dot\gamma(t)\rangle_g}\,\mathrm{d}t. \end{equation}\) Here, we follow the convention to use Newton’s notation to denote derivatives with respect to $t$.
Geodesic, Exponential Map & Logarithm Map
In Euclidean geometry, there is one specific family of curves that are crucial for establishing the standard geometry: the straight lines. In Riemannian manifold, we naturally want to extend the idea of straight lines to curved spaces. So again, imagine you are a tiny ant on the manifold. As the manifold is locally flat, you can follow the direction of some tangent vector and go straight while maintaining the same direction and constant speed on the manifold. The route you have traced is a straight line on the manifold, which is called a geodesic.
One fundamental results for geodesics is the local existence and uniqueness theorem, which states that for any point $x\in\mathcal{M}$ and any tangent vector $u\in T_x\mathcal{M}$, there exists a unique geodesic $\gamma:[0,T]\to\mathcal{M}$ such that $\gamma(0)=x$ and $\dot\gamma(0)=u$. There are some interesting properties of geodesics as the straight lines on the Riemannian manifold. One of the most mentioned properties is that the geodesic is the locally distance minimizing curve. This can be understood as the generalization of the well-known result from elementary school that, in the Euclidean space, the shortest path between two points is the straight line segment. This property can be also understood as the kinetic energy minimizing curve, with the energy functional defined as: \(\begin{equation} E(\gamma)=\frac{1}{2}\int_0^Tg_{\gamma(t)}(\dot\gamma(t),\dot\gamma(t))\,\mathrm{d}t. \end{equation}\) Using the classical calculus of variations techniques, one can derive the geodesic equation for explicitly solving the geodesic $\gamma(t)$, which we will omit here. The geodesic distance $d_g(x,y)$ between two points $x,y\in\mathcal{M}$ is defined as the length of the globally length-minimizing curve that connects $x$ and $y$. As the globally optimum always ensures the local optimum, the geodesic distance is always the curve length of some geodesic. However, the inverse is not necessarily true, i.e., the curve length of a geodesic connecting two points is not necessarily the geodesic distance.
Length-minimizing property
One common misunderstanding is that the geodesic is the globally shortest path between any two points on the manifold. This is not true in general. For example, consider the sphere whose geodesics are the great circles. For a pair of non-antipodal points, the great circle is cut into a shorter arc and a longer arc, both of which are geodesics. However, only the shorter path is the globally shortest path. Another example is provided below. Nonetheless, globally optimum is always guaranteed for geodesic distance as a result of its definition.
More general definition
Contrary to other standard approach that deduce the geodesic from the locally length-minimizing property, I adopt the definition that relies on a dynamics in which the point travels at a constant speed. It turns out that the definition of constant tangent vectors is non-trivial, as the tangent spaces are different for different points. Eventually, this idea of defining constant tangent vectors leads to the concepts of parallel transport, affine connection, and the general definition of affine geodesic. For general affine geodesics, the locally length-minimizing property no longer holds. In contrast, the standard locally length-minimizing geodesic is a special case of the affine geodesic, which is known as the Levi-Civita geodesic. The Levi-Civita geometry is uniquely defined by the Riemannian metric and is therefore also referred to as the canonical Riemannian structure.The exponential map $\exp:\mathcal{M}\times T\mathcal{M}\to \mathcal{M}$ answers the questions that, after traveling for a unit time with a constant direction and speed, what point will you reach on the manifold. Formally, for a point $x\in\mathcal{M}$ and a tangent vector $u\in T_x\mathcal{M}$, the exponential map is defined as: \(\begin{equation} \exp_x(u):=\gamma(1), \end{equation}\) where $\gamma$ is the unique geodesic that satisfies $\gamma(0)=x$ and $\dot\gamma(0)=u$. The logarithm map $\log:\mathcal{M}\times\mathcal{M}\to T\mathcal{M}$ is the inverse of the exponential map, which answers the question that, given two points on the manifold, what is the direction and distance one need to travel to reach one point from the other. Formally, for two points $x,y\in\mathcal{M}$, the logarithm map is defined such that the following identity always holds: \(\begin{equation} \exp_x(\log_x y)\equiv y . \end{equation}\)
Based on the idea of constant speed dynamics, we have $\|\dot\gamma(t)\|_g\equiv\|\dot\gamma(0)\|_g=\|u\|_g$. In this scenario, we have \(\begin{equation} \|\log_x (y)\|_g=L(\gamma_{x,y}), \end{equation}\) where $L(\gamma_{x,y})$ is the length of the geodesic $\gamma_{x,y}$ that connects $x$ and $y$. If the uniqueness of the geodesic is globally guaranteed, we further have $\|\log_x (y)\|_g=d_g(x,y)$. Simiarly, based on the idea of dynamic, the geodesic interpolation between two points $x,y\in\mathcal{M}$ is defined as $\gamma_{x,y}(t)$ for $t\in[0,1]$. Using the exponential and logarithm map, the geodesic interpolation can be compactly written as: \(\begin{equation} \gamma(t)=\exp_x(t\log_x y). \end{equation}\)
When does the assumption hold?
For the canonical Riemannian structure induced by the Levi-Civita connection, the assumption $\|\dot\gamma(t)\|_g\equiv\|\dot\gamma(0)\|_g$ always holds. For general affine connection, it is not guaranteed. In most cases, we work with the canonical Riemannian structure in this post.Some caveats
- There might be scenarios when $T<1$ for the existence and uniqueness theorem to hold. This means that the exponential map may not be well-defined for all tangent vectors. Nonetheless, we can always scale the tangent vector accordingly for a larger $T$.
- The global uniqueness of geodesic between any two points on the manifold is not guaranteed. For example, consider a pair of antipodal points on a sphere, there are infinite many great circles that have the same length. In this scenario, the logarithm map is not well-defined.
The Riemannian norm and geodesic interpolation are the crucial concepts in Riemannian flow matching, in which the probability paths are defined along the geodesics. From the next section, I will dig into some commonly encountered Riemannian manifolds in machine learning tasks.
Euclidean Space
Of course, as Riemannian manifold is modeling as a generalization of the Euclidean space $\mathbb{R}^n$, the first thing we will do it naturally test its compatibility with our common intuition in the latter. The Riemannian metric is the standard Euclidean inner product: \(\begin{equation} g_x(u,v)=\langle u,v\rangle=\sum_{i=1}^n u_i v_i. \end{equation}\) Similarly, the Riemannian norm is the standard Euclidean norm $\|\cdot\|_2$. As we can travel in the Euclidean space without obstacles, the exponential map on the Euclidean space simple translate the base vector with the tangent vector. The exponential and logarithm maps, therefore, can be easily computed as: \(\begin{align} \exp_x(u)&=x+u,\\ \log_x(y)&=y-x. \end{align}\) Similarly, the geodesic interpolation is the linear interpolation between two points: \(\begin{equation} \gamma(t)=tx+(1-t)y. \end{equation}\)
Wait ... How about the exponential function?
If you came up with this question, then probably you are a math enthusiast! The exponential map reads a linear function of $u$, whereas the standard exponential function reads $\exp u=e^u$. Wait! We've got a conflict even on the Euclidean space!
It turns out that we need to consider an alternative Riemannian manifold to resolve this conflict. Consider the manifold of positive real numbers $\mathbb{R}_+$. At each point $x\in\mathbb{R}_+$, the tangent space is identified with $T_x\mathbb{R}_+\cong\mathbb{R}$. We can use the Riemannian metric: $$ g_x(u,v)=\frac{uv}{x^2},\quad x\in \mathbb{R}_+,u,v\in T_x\mathbb{R}_+. $$ We now verify that the following geodesic $$ \gamma(t)=e^{ut} $$ satisfied the constant speed requirement with the initial condition of $\gamma(0)=1,\dot\gamma(0)=u$. We first note that $\dot\gamma(t)=u e^{ut}=u\gamma(t)$, which satisfies the initial condition. Calculating the Riemannian norm, we have: $$ g_{\gamma(t)}(\dot\gamma(t),\dot\gamma(t))=g_{\gamma(t)}(u\gamma(t),u\gamma(t))=\frac{u^2\gamma(t)^2}{\gamma(t)^2}=u^2. $$ In this way, we always have $\|\dot\gamma(t)\|^2_g=u^2$, which is independent of the time $t$. Therefore, the curve $\gamma(t)$ is indeed a geodesic. Setting $t=1$ recovers the exponential map as $\exp_1(u)=e^u$, which coincides with the standard exponential function.
Why this metric?
You probably wonder why we are using such an exotic Riemannian metric on $\mathbb{R}_+$. It turns out that, as $\mathbb{R}_+$ is a Lie group — a differential manifold that is also a group, — there is a canonical way of choosing the metric such that it should be bi-invariant. We know the group structure of $\mathbb{R}_+$ is well-defined with the standard multiplication, which means the bi-invariant metric on $\mathbb{R}_+$ is invariant to scaling: $$ g_{\lambda x}(\lambda u,\lambda v)=g_x(u,v),\quad x\in\mathbb{R}_+,u,v\in T_x\mathbb{R}_+. $$ It is easy to verify that the metric $g_x(u,v)=\frac{uv}{x^2}$ satisfies the bi-invariant property, whereas the standard Euclidean metric does not. In this case, we are essentially using the logarithmic coordinates to represent the positive real numbers. Therefore, at each point $x\in\mathbb{R}_+$, the local coordinate in the target space should be $u/x$, which represents the relative scaling under the group operation of multiplication and also leads to the bi-invariant metric.
This bi-invariant property is important for drawing the connection between the Lie group, the Riemannian manifold, and the Lie algebra. The exponential map $\exp:\mathbb{R}\to \mathbb{R}_+$ converts an element in the Lie algebra to the Lie group, and the logarithm map $\log:\mathbb{R}_+\to \mathbb{R}$ converts an element in the Lie group to its Lie algebra. We will also see this important relationship in the 3D rotation group, another well-known Lie group.
Alternative interpretation
We can also provide an alternative interpretation to resolve the conflict between the exponential map and the exponential function by considering general affine geodesics. Recall that affine geodesics are defined by the dynamics in which the point travels at a constant speed. Let's fix our start point to $x=1$ and consider the tangent vector $u\in\mathbb{R}$. Now consider the following two definitions of constant speed:
- At each time step, the speed should also be $u$.
- At each time step, the speed should be proportional to the current position.
In the second definition, the speed of traveling is $u\gamma(t)$ to be considered constant, — weird but valid! The first definition gives the following differential equation: $$ \dot\gamma(t)=u,\quad \gamma(0)=1, \dot\gamma(0)=u, $$ which gives the solution $\gamma(t)=1+ut$ and the exponential map of $\exp(u)=1+u$. The second definition gives the following differential equation: $$ \dot\gamma(t)=u\gamma(t),\quad \gamma(0)=1, \dot\gamma(0)=u, $$ which gives the solution $\gamma(t)=e^{ut}$ and the exponential map of $\exp(u)=e^u$. This indicates that the exponential function can also interpret as the exponential map of some affine geodesic.
Flat Torus
We now continue to explore the flat torus $\mathbb{T}^n$. For simplicity and better visualization, let’s first consider $n=2$, which is often visualized as a doughnut embedded in the 3D Euclidean space. This, however, is actually not an accurate representation when we consider their geometric properties. As its name indicated, a flat torus have zero Gaussian curvature everywhere, meaning it is essentially a flat plane without any bending or stretching. In contrast, the embedded 2D torus has non-zero curvatures at different points, which can be verified by gluing opposite edges of a square paper. One can easily roll a flat paper into a cylinder which also has zero curvature, but it is impossible to further roll the cylinder into a doughnut without stretching or bending the paper.
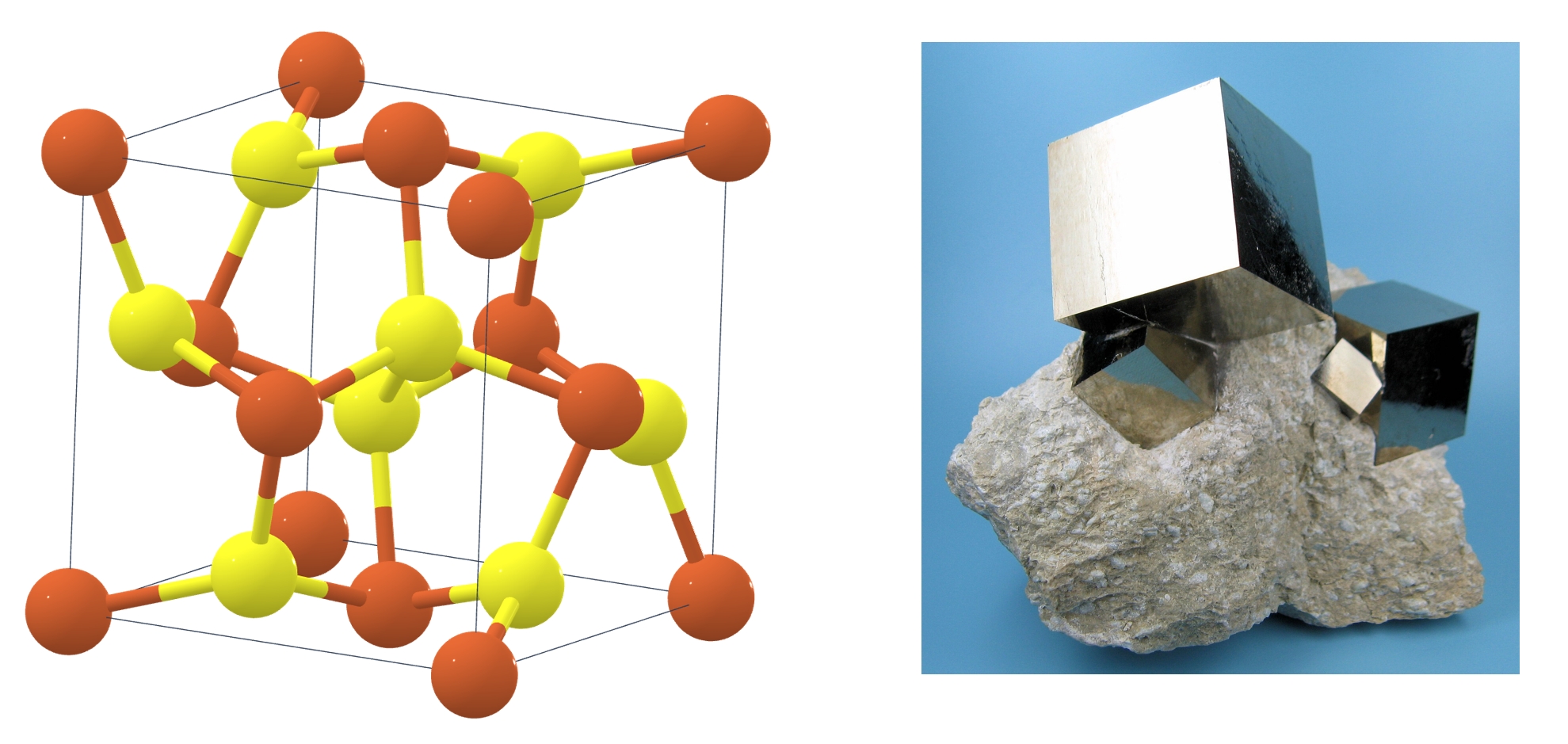
Therefore, it is better to understand a flat torus as a quotient space of the Euclidean space $\mathbb{R}^n$ by the lattice $\mathbb{Z}^n$ as $\mathbb{T}^n=\mathbb{R}^n/\mathbb{Z}^n$. In other words, in the 2D case, we consider the following equivalence class by identifying points that differ by integer translations in two independent directions: \(\begin{equation} (x,y)\sim (x+m,y+n),\quad m,n\in\mathbb{Z}. \end{equation}\) Such an identification can be understood visually as gluing the opposite sides of a square with the same direction, as demonstrated in . A better example to understand the flat torus is the crystal structure. In crystallography, the crystal structure is often represented as a unit cell, the smallest repeating unit. With periodic boundary conditions, the unit cell can be extended to the whole crystal structure, which is essentially a 3D flat torus (see ).
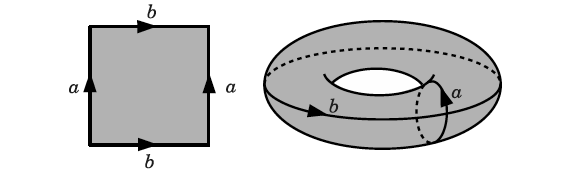
It is also possible to define the quotient space with respect to other values, such as the cell length of a unit cell, or $2\pi$ for a torsion angle as a rotation of $2\pi$ is equivalent to no rotation. Nonetheless, it is simpler to use fractional coordinates such that any coordinate always lies in $[0, 1)$. We will use this assumption in the following discussion.
About the different tori
We distinguish the flat torus from the embedded torus because we care about their geometric properties in differential geometry. If we consider topological properties, these two tori are indeed equivalent (more precisely, they are homeomorphic). Homeomorphism allows us to bend and stretch manifolds when drawing equivalence.One choice to identify the tangent space of the flat torus is also to limit each component of the tangent vector to $[0, 1)$. In this way, we have $T_x\mathbb{T}^n\cong \mathbb{T}^n$. As a quotient space of the Euclidean space, the flat torus inherits the Euclidean metric and Euclidean norm. Therefore, the common straight lines are geodesics on the flat torus. The exponential and logarithm maps can be easily computed as: \(\begin{align} \exp_x(u)&=x+u \mod 1,\\ \log_x(y)&=y-x \mod 1, \end{align}\) which is essentially the same as the Euclidean space except for the additional modulo operation. Simiarly, the geodesic interpolation only differs with the additional modulo. However, we should be careful when computing the Riemannian norm in the tangent space. Consider the target vector field of $u=0.1$. For two predictions $v_1=0.5,v_2=0.9$, it turns out that $v_2$ is closer to the target vector due to the periodicity in the exponential map. We shall follow the minimum image convention to select the shortest path between two points. In this way, the Riemannian norm should be calculated as: \(\begin{align} \|u\|_\mathbb{T}=\left\|\min \{u,1-u\}\right\|_2,\quad u\in T\mathbb{T}^n=[0,1)^n. \label{eqn:torus-norm} \end{align}\) where the minimum operation is element-wise.
Alternative parameterization
There exists an alternative parameterization of the flat torus that models the tangent vector as angles $u\in(-\pi,\pi]^n$. Essentially, this parameterization try to find the direction of the straight line that connects $x$ to $y$. The exponential and logarithm maps can be computed as: $$ \begin{align*} \exp_x(u)&=x+u/(2\pi)\mod 1,\\ \log_x(y)&=\operatorname{atan2}(\sin 2\pi(y-x), \cos 2\pi(y-x)), \end{align*} $$ where $\mathrm{atan2}$ is the 2-argument arctangent function that automatically wraps the direction in the Cartesian plane to $(-\pi,\pi]$. Such a parameterization makes sure that the vector field returned by the logarithm map follows the minimum image convention, i.e., it always represents the shortest direction between two points. Still, we need to follow the similar procedure to wrap the difference of the angles to $(-\pi,\pi]$ when calculating the norm.
Spherical Manifold (Unfinished)
The previous two manifolds are flat manifolds with relatively intuitive and simple geometries. We now move to the spherical manifold $S^n=\{x\in\mathbb{R}^{n+1}:\|x\|_2=1\}$. $S^n$ is an $n$-dimensional manifold embedded in the $(n+1)$-dimensional Euclidean space. As its name indicates, we often visualize $S^2$ as a sphere, the surface of a 3D ball (see ).

Intuitively, the tangent space at a point on the sphere $x\in S^n$ can be identified as the hyperplane perpendicular to the vector $x$: $T_xS^n=\{u:\langle u,x\rangle=0\}$. As an embedded manifold, $S^n$ inherits the ambient Euclidean metric. Therefore, the spherical metric is exactly the same as the Euclidean one: \(g_x(u,v)=\langle u,v\rangle.\)